概览

本片博客将介绍以下内容

单链表的结构；
单链表中执行遍历，插入和删除操作；
单链表中不同操作的时间复杂度。

单链表的简介

链表是一种线性数据结构，它通过引用字段将所有分离的元素链接在一起。

下面是一个单链表的例子：

蓝色箭头显示单个链接列表中的结点是如何组合在一起的。

单链表的节点结构

// Definition for singly-linked list.
public class SinglyListNode {
    int val;
    SinglyListNode next;
    SinglyListNode(int x) { val = x; }
}

在大多数情况下，我们将使用头结点(第一个结点)来表示整个列表。

添加操作 - 单链表

如果我们想在给定的结点 prev 之后添加新值，我们应该：

使用给定值初始化新结点 cur；
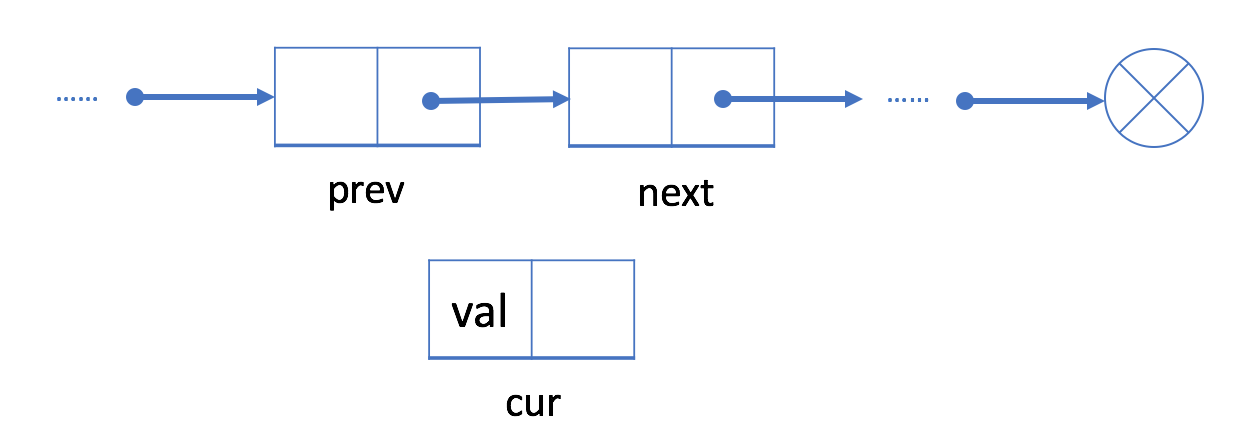
将 cur 的“next”字段链接到 prev 的下一个结点 next；
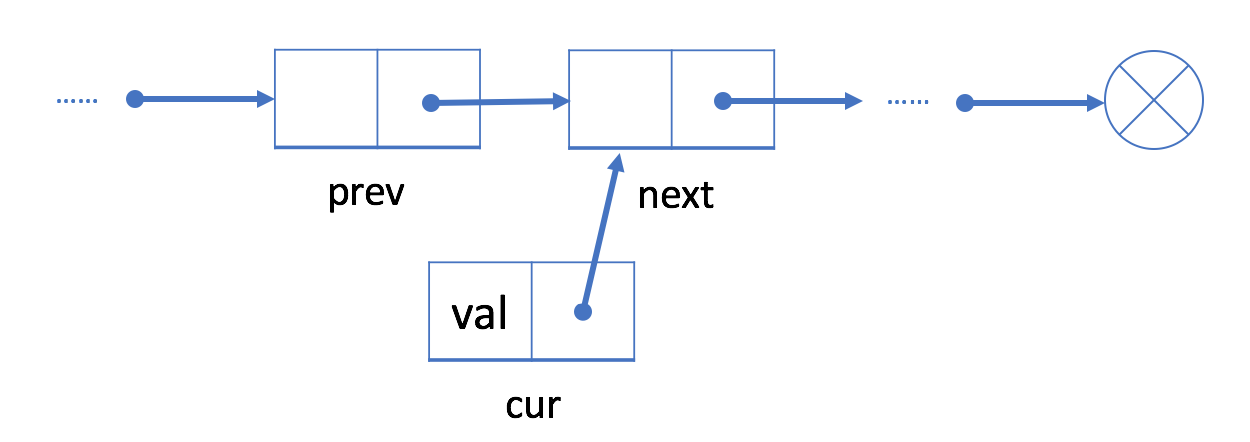
将 prev 中的“next”字段链接到 cur 。

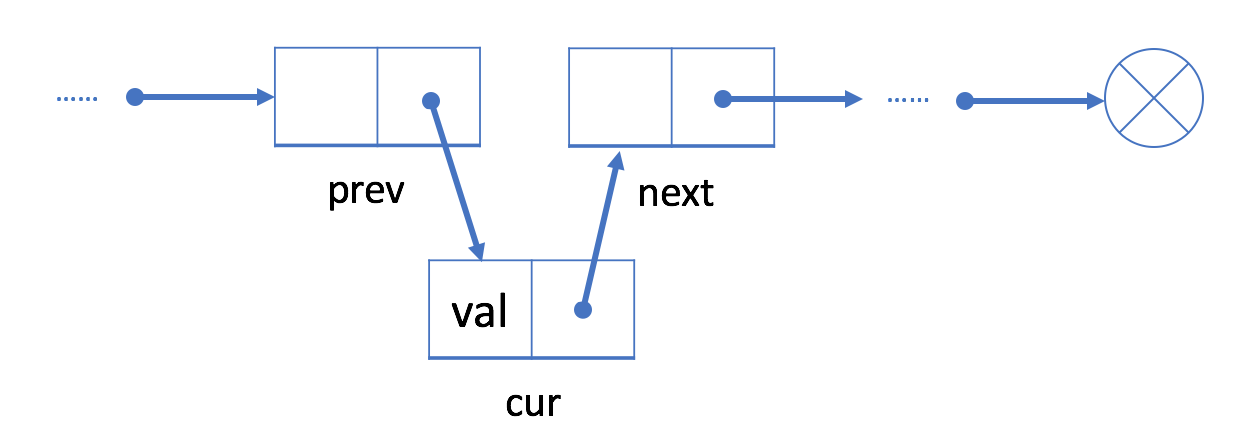
与数组不同，我们不需要将所有元素移动到插入元素之后。因此，您可以在 O(1) 时间复杂度中将新结点插入到链表中，这非常高效。

示例

让我们在第二个结点 6 之后插入一个新的值 9。

我们将首先初始化一个值为 9 的新结点。然后将结点 9 链接到结点 15。最后，将结点 6 链接到结点 9。

插入之后，我们的链表将如下所示：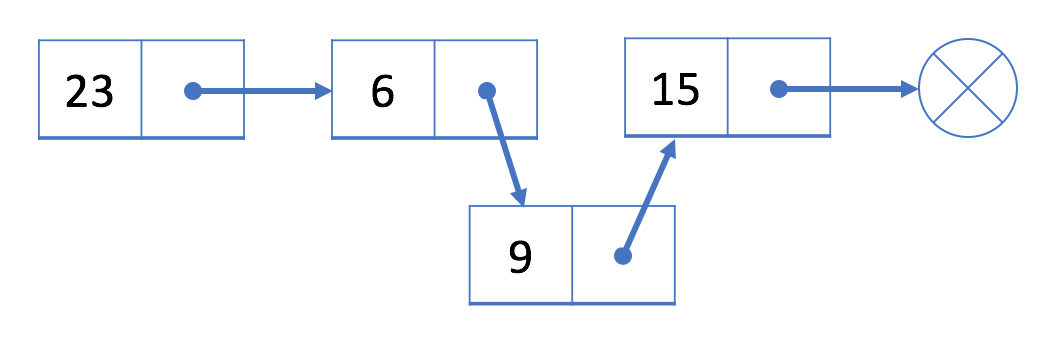

在开头添加结点

众所周知，我们使用头结点来代表整个列表。

因此，在列表开头添加新节点时更新头结点 head 至关重要。

初始化一个新结点 cur；
将新结点链接到我们的原始头结点 head。
将 cur 指定为 head。

例如，让我们在列表的开头添加一个新结点 9。

我们初始化一个新结点 9 并将其链接到当前头结点 23。
指定结点 9 为新的头结点。

删除操作 - 单链表

如果我们想从单链表中删除现有结点 cur，可以分两步完成：

找到 cur 的上一个结点 prev 及其下一个结点 next；
接下来链接 prev 到 cur 的下一个节点 next。

在我们的第一步中，我们需要找出 prev 和 next。使用 cur 的参考字段很容易找出 next，但是，我们必须从头结点遍历链表，以找出 prev，它的平均时间是 O(N)，其中 N 是链表的长度。因此，删除结点的时间复杂度将是 O(N)。

空间复杂度为 O(1)，因为我们只需要常量空间来存储指针。

示例

让我们尝试把结点 6从上面的单链表中删除。

从头遍历链表，直到我们找到前一个结点 prev，即结点 23
将 prev（结点 23）与 next（结点 15）链接

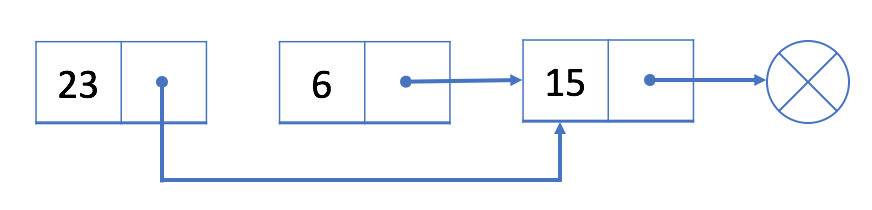
结点 6 现在不在我们的单链表中。

删除第一个结点

如果我们想删除第一个结点，策略会有所不同。

正如之前所提到的，我们使用头结点 head 来表示链表。我们的头是下面示例中的黑色结点 23。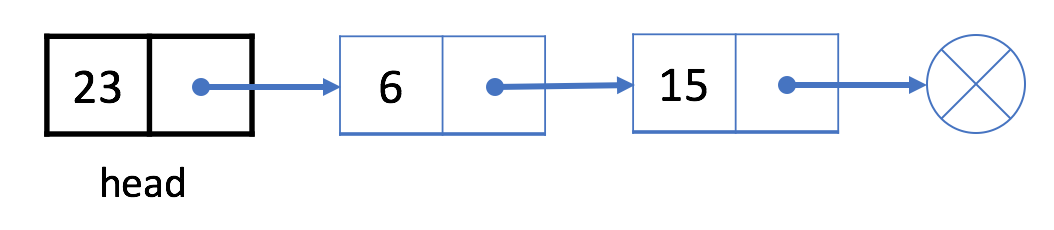

如果想要删除第一个结点，我们可以简单地将下一个结点分配给 head。也就是说，删除之后我们的头将会是结点 6。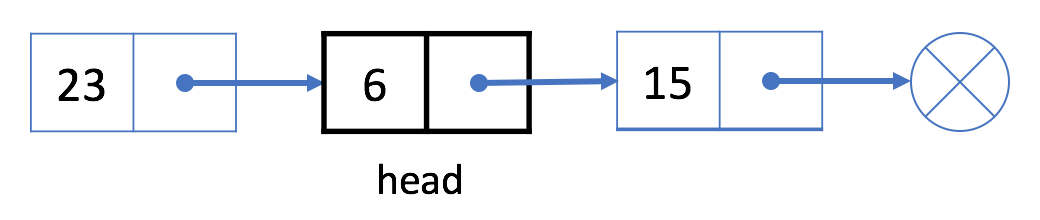

链表从头结点开始，因此结点 23 不再在我们的链表中。

单链表java实现

实现单链表数据结构

public class Node{
        Int data;
        Node next;
        public Node(){
        this.next = null;
        }
}

头插法建立链表


public Node insert_head(int[] arr,Node h){      
for(int i = 0; i < arr.length; i++){
    Node p = new Node();
    p.data = arr[i];
    p.next = h.next;//改变指针
    h.next = p;//使h的直接后继为p
    }
    return h.next;//去掉伪结点
    }

获取单链表长度

public static int size(Node h) {
        if (h == null) {
            return 0;
        } else {
            int count = 1;
            Node p = h.next;
            while (p != null) {
                count++;
                p = p.next;
            }
            return count;
        }
    }

插入一个节点


public static Node insert(int data, Node p) {
        Node x = new Node();
        x.data = data;
        if (p == null) {
            p = x;
        } else {
            x.data = data;
            x.next = p.next;
            p.next = x;
        }
        return p;
    }

删除一个结点


public Node remove(Node h) {
        Node p;
        if (h != null && h.next != null) {
            p = h.next;
            h.next = p.next;//指向p的直接后继结点
            return h;
        } else {
            return null;
        }
    }

按值查找结点


public static Node search(int data, Node h) {
        if (h == null) {
            return null;
        } else if (h.next == null) {
            return h;
        } else {
            Node p = h.next;
            while (p.data != data) {
                p = p.next;
            }
            return p;
        }
    }

遍历链表

public void display(Node h) {
        if (h == null) {
            System.out.println("h is null");
        } else if (h.next == null) {
            System.out.print(h.data);
        } else {
            while (h != null) {
                System.out.print(h.next.data + " ");//不遍历头结点
                h = h.next;
            }
        }
    }