我们可以这样去求逆矩阵:
- 一、求余子式矩阵,
- 二、转成代数余子式矩阵,
- 三、转成伴随矩阵,
- 四、乘以 1/行列式。
最好是用实例来解释!
例子:求 A 的逆:
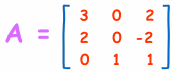
要做四步。全都是简单的算术,但有很多计算,所以要小心,不要犯错!
一、余子式矩阵
第一步是造一个 “余子式矩阵”。这步有最多计算。
为矩阵的每个元素:
- 不使用在本行与本列的元素
- 计算剩下来的值的行列式
把行列式的结果放进一个矩阵(”余子式矩阵”)
行列式
2×2 矩阵(2行和2列)的行列式很容易:ad-bc
| 想:十字乘法蓝色 代表 正 (+ad),红色 代表 负 (-bc) | 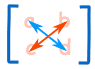 |
|
|---|---|---|
(3×3 矩阵会比较复杂,。。。。。。)
计算
这是”余子式矩阵“的头两个和最后两个计算(留意我不使用在元素本行和本列的值,只用剩下来的值来算行列式):
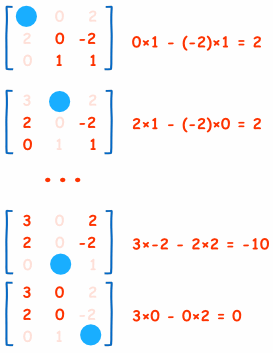
这是整个矩阵的计算程序:
二、代数余子式矩阵
这个容易!把”纵横交错”排列的正负号放在”余子式矩阵”上。换句话说,我们需要每隔一个格改变正负号,像这样:
三、伴随
“转置” 以上的矩阵。。。。。。就是沿对角线对调元素的位置(在对角线上的元素不变):
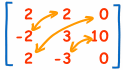
四、乘以 1/行列式
求原本的矩阵的行列式。这不困难,因为在求”余子式矩阵”时我们已经计算了局部的行列式。
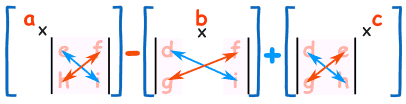
所以:把顶行的每个元素乘以其”余子式”的行列式:
行列式 = 3×2 - 0×2 + 2×2 = 10
现在把伴随矩阵乘以 1/行列式:
大功告成!
把这答案与在 用初等行运算来求逆矩阵 里求的逆矩阵比较一下。是不是一样?你喜欢哪个方法?
较大的矩阵
求更大的矩阵的逆矩阵都是用同样的方法(例如 4×4 和 5×5等),可是,真的要做很多很多的计算!
4×4 矩阵要做 16个 3×3 行列式。所以通常是用电脑来做(例如 矩阵计算器。)
结论
- 为每个元素,计算不在其本行或本列 的值 的行列式 来构成余子式矩阵
- 把纵横交错排列的正负号放在”余子式矩阵”上以形成代数余子式矩阵
- 转置矩阵以成为伴随矩阵
- 乘以 1/行列式 以成为逆矩阵



