矩阵是数的排列
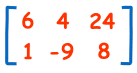
矩阵
(这矩阵有2行和3列)
把矩阵与一个数相乘是容易的:
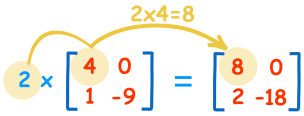
计算是这样的:
| 2×4=8 | 2×0=0 |
|---|---|
| 2×1=2 | 2×-9=-18 |
我们叫这个数 (”2”)为标量,所以这乘法被称为”标量乘法”.
矩阵与矩阵相乘
但若要把矩阵与矩阵相乘,我们要计算行与列的”点积“……这是什么意思?我们来看个例子:
求 第一行 和 第一列 的答案:
“点积” 是把 对称的元素相乘,然后把结果加起来:
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58
我们把第一个元素相配(1 和 7),然后相乘。第二个元素(2 和 9) 和第三个元素(3 和 11)也一样,然后把结果加起来。
想多看一个例子?这是第一行与第二列:
(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64
第二行 和 第一列也同样做:
(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139
第二行 和 第二列:
(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154
我们得到:
做好了!
为什么要这样做?
乍看像个过于复杂的乘法,但这是有道理的!
看看一个实例:
例子:饼店卖三种派。
- 牛肉派卖¥3一个
- 鸡肉派卖¥4一个
- 素菜派卖¥2一个
这是过去4天里饼店卖的数目:
现在来想想……星期一的销售额是这样算出来的:
牛肉派的销售额 + 鸡肉派的销售额 + 素菜派的销售额
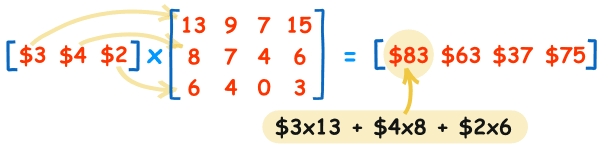
$3×13 + $4×8 + $2×6 = $83
总销售额是价钱与销售量的点积:
($3, $4, $2) • (13, 8, 6) = ¥3×13 + ¥4×8 + ¥2×6 = ¥83
我们把价钱和销售量相配,把它们逐个相乘,然后把结果 加起来。
换句话说:
- 星期一的销售额是:牛肉派:¥3×13=¥39,鸡肉派:¥4×8=¥32,素菜派:¥2×6=¥12。总共是 ¥39 + ¥32 + ¥12 = ¥83
- 星期二的销售额是:¥3×9 + ¥4×7 + ¥2**×4 = ¥63**
- 星期三的销售额是:¥3×7 + ¥4×4 + ¥2**×0 = ¥37**
- 星期四的销售额是:¥3×15 + ¥4×6 + ¥2**×3 = ¥75**
所以重点是要把价钱和销售量正确地相配。
明白为什么要用”点积”了吗?
用矩阵写出来是这样:
星期一卖了¥83的派,星期二¥63,……
(你可以把这些值打进矩阵计算器来看看。)
行与列
要表达一个矩阵有几行和几列,我们通常写 行×列。
例子:这是个 2×3 矩阵(2行和3列):
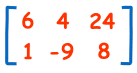
把两个矩阵相乘时:
- 第一个矩阵的列数必须是等于第二个矩阵的行数。
- 相乘的结果具有第一个矩阵的 行数 和第二个矩阵的 列数。
例子:

在这例子里,我们把 1×3 矩阵乘以 3×4 矩阵(留意两个矩阵都有 3),相乘的结果是个 1×4矩阵。
一般来说:
把m×n矩阵与n×p矩阵相乘,n 必须相同,
相乘结果是m×p矩阵。

乘法的次序
在算术里我们知道:
3 × 5 = 5 × 3
(乘法的互换律)
但在矩阵的领域这通常是不正常的(矩阵乘法并非可互换):
AB ≠ BA
当乘法的次序改变,答案亦(通常)改变。
例子:
来看看次序怎样影响这矩阵相乘:
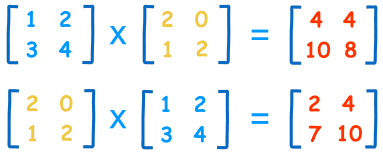
单位矩阵
“单位矩阵” 是矩阵领域里的 “1”:
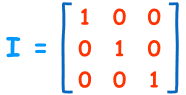
3x3 单位矩阵
- 单位矩阵是”方形”的(行与列数目相同),
- 对角线全是1,其他全是0。
- 符号为大写字母 I。
它是个特别的矩阵,因为把它和一个矩阵相乘,后者不变:
A × I = A
I × A = A




