矩阵

矩阵是数的排列：

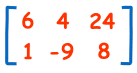
矩阵
（这矩阵有2行和3列）

我们可以用矩阵来做很多。。。。。。

加

把两个矩阵相加：把对称位置的数相加：

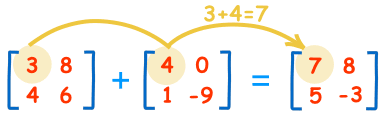
计算是这样：

3+4=7	8+0=8
4+1=5	6-9=-3

两个矩阵一定要大小相同，就是说，行要一样大小，列也要一样大小。

例子：具有3 行 和 5 列 的矩阵可以和另一个有 3 行 和 5 列的矩阵相加。

但它不能和有 3 行 和 4 列 的矩阵相加（列的大小不同）

负矩阵

负矩阵也很简单：

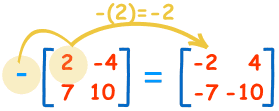
计算是这样：

-(2)=-2	-(-4)=+4
-(7)=-7	-(10)=-10

减

把两个矩阵相减：把对称位置的数相减：

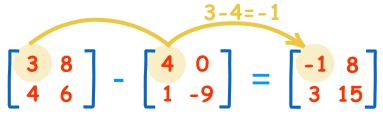
计算是这样：

3-4=-1	8-0=8
4-1=3	6-(-9)=15

注意：矩阵减法的定义实际是与负矩阵相加： A + (-B)

乘以常数

我们可以把矩阵乘以常数：

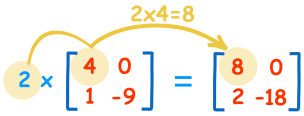
计算是这样：

2×4=8	2×0=0
2×1=2	2×-9=-18

我们称这常数为 标量，故此这乘法的正式名字是 “标量乘法”.

与另一个矩阵相乘

把两个矩阵相乘 是有点复杂。。。。。。请去矩阵乘法看看怎样做。

除法

那除法呢？实际上，我们不把矩阵相除，我们这样做：

A/B = A × (1/B) = A × B-1

其中 B-1 是 B 的 “逆矩阵”。

所以我们不做除法，我们乘以逆矩阵。

计算逆矩阵要用特别的方法。。。。。。

。。。。。。去逆矩阵了解更多。

矩阵转置

去”转置” 一个转置，把行和列对换。 我们在右上角放一个 “T” 来代表转置：

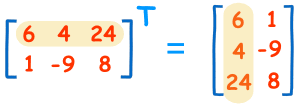
记号法

我们通常用英语大写字母（例如 A 或 B）来代表矩阵

矩阵里的每个数（”元素”）以小写字母来代表，并带上表示 “行，列“ 的 “下标数”：

	行与列哪个是行？哪个是列？行 从 左至右列 从 上至下

例子：

B =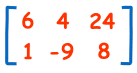

这是一些例子：

b1,1 = 6 （在行 1，列 1 的元素是 6）

b1,3 = 24 （在行 1，列 3 的元素是 24）

b2,3 = 8 （在行 2，列 3 的元素是 8）